原创：量化投资选股的python程序实践

liyonghua   2016年12月9日   技术研究   评论(0)   浏览(2826)  

首先选取沪深股票市场，本人比较关注的12只股票：

000002 万科A，600566 济川药业，300051 三五互联，002039 黔源电力，600872 中炬高新，300324 旋极信息，600885 宏发股份，600382 广东明珠，000732 泰和集团，002174 游族网络，000915 山大华特，002415 海康威视

备注： 如果是基金经理，则会有研究部门推荐的股票选择池

 

 

程序运行的得到结论如下：

1.    当投资组合的sharpe值最大时，投资组合为：

41.2%的万科A，10.5%的广东明珠，38.2%的山大华特，10.1%的海康威视

该组合的未来预期年化收益为：21.4%

该组合的预期年化波动率为：29.5%

该组合的sharpe指数为0.725

 

2.    当投资组合的波动最小时，投资组合为：

34.5%的万科A，17.9%的济川药业，24.6%的黔源电力，2%的旋极信息，1%的宏发股份，9.4%的泰和集团，0.8%的游族网络，9.8%的海康威视

该组合的未来预期年化收益为：3.7%

该组合的预期年化波动率为：22.6%

该组合的sharpe指数为0.163

 

相关输出图表如下：

图1：关注的12只股票从2016-01-01到2016-12-01的归一化股价走势

 

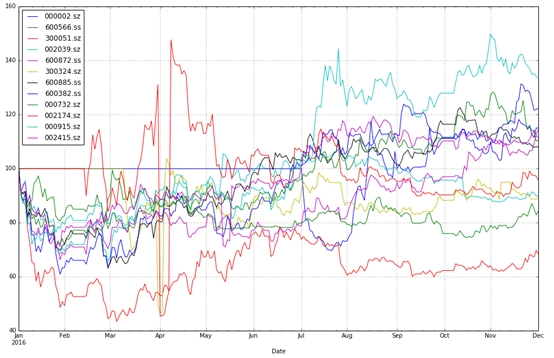
图2：10万次蒙特卡洛模拟计算，得到各种投资组合以及相应收益率和波动率

 

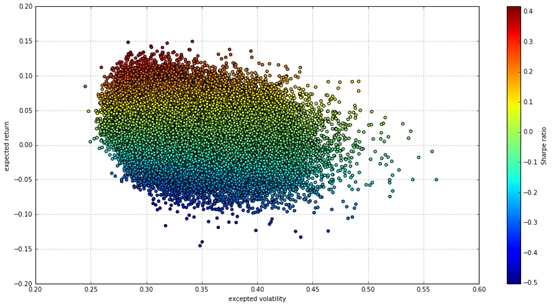
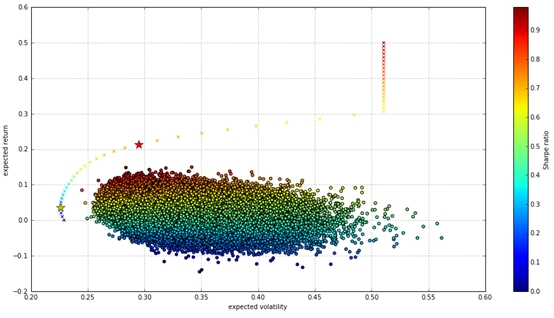
图3：有效前沿、最优投资组合的图

#叉号：构成的曲线是有效前沿（efficient frontier，目标收益率下最优的投资组合）

#红星：夏普值最大的投资组合

#黄星：方差最小的投资组合

程序源代码以及详细注释说明如下：

1. # -*- coding: utf-8 -*-  
2. """ 
3. Created on Thu Dec  8 01:26:52 2016 
4.  
5. @author: Administrator 
6. """  
7.   
8. import pandas as pd  
9. import numpy as np  
10. #import statsmodels.api as sm #统计运算  
11. #import scipy.stats as scs #科学计算  
12. import matplotlib.pyplot as plt #绘图  
13. import pandas.io.data as web  
14. #import tushare as ts  
15.   
16.   
17. # 1.选取感兴趣的股票  
18.   
19. # 000002 万科A，600566 济川药业，300051 三五互联，002039 黔源电力，600872 中炬高新，300324 旋极信息，600885 宏发股份，600382 广东明珠，000732 泰和集团，002174 游族网络，000915 山大华特，002415 海康威视  
20. # 并比较一下数据（2016-01-01至2016-12-01）  
21.   
22. symbols = ['000002.sz','600566.ss','300051.sz','002039.sz','600872.ss','300324.sz',
23. '600885.ss','600382.ss','000732.sz','002174.sz','000915.sz','002415.sz']  
24.   
25. noa = len(symbols)  
26.   
27. data = pd.DataFrame()  
28. for sym in symbols:  
29.     data[sym] = web.DataReader(sym, data_source='yahoo',start='2016-01-01',  
30.                                end='2016-12-01')['Adj Close']  
31. data.columns = symbols  
32.   
33. data.head(5)  
34.   
35. (data / data.ix[0] * 100).plot(figsize=(16, 10), grid=True)  
36.   
37.   
38. #2.计算不同证券的均值、协方差  
39. #每年252个交易日，用每日收益得到年化收益。计算投资资产的协方差是构建资产组合过程的核心部分。运用pandas内置方法生产协方差矩阵。  
40. returns = np.log(data / data.shift(1))  
41.   
42. returns.mean()*252  
43.   
44. returns.cov()*252  
45.   
46.   
47. #3.给不同资产随机分配初始权重  
48. #由于A股不允许建立空头头寸，所有的权重系数均在0-1之间  
49. weights = np.random.random(noa)  
50.   
51. weights /= np.sum(weights)  
52.   
53. weights  
54.   
55.   
56. # 4.计算预期组合年化收益、组合方差和组合标准差  
57. np.sum(returns.mean()*weights)*252  
58.   
59. np.dot(weights.T, np.dot(returns.cov()*252,weights))  
60.   
61. np.sqrt(np.dot(weights.T, np.dot(returns.cov()* 252,weights)))  
62.   
63.   
64. # 5.用蒙特卡洛模拟产生大量随机组合  
65. #进行到此，我们最想知道的是给定的一个股票池（证券组合）如何找到风险和收益平衡的位置。  
66. #下面通过一次蒙特卡洛模拟，产生大量随机的权重向量，并记录随机组合的预期收益和方差。  
67.   
68. port_returns = []  
69.   
70. port_variance = []  
71.   
72. for p in range(100000):  
73.   
74.     weights = np.random.random(noa)  
75.       
76.     weights /=np.sum(weights)  
77.   
78.     port_returns.append(np.sum(returns.mean()*252*weights))  
79.   
80.     port_variance.append(np.sqrt(np.dot(weights.T, np.dot(returns.cov()*252, weights))))  
81.   
82. port_returns = np.array(port_returns)  
83.   
84. port_variance = np.array(port_variance)  
85.   
86. #无风险利率设定为3%  
87.   
88. risk_free = 0.03  
89.   
90. plt.figure(figsize = (16,8))  
91.   
92. plt.scatter(port_variance, port_returns, c=(port_returns-risk_free)/port_variance, marker = 'o')  
93.   
94. plt.grid(True)  
95.   
96. plt.xlabel('excepted volatility')  
97.   
98. plt.ylabel('expected return')  
99.   
100. plt.colorbar(label = 'Sharpe ratio')  
101.   
102.   
103. #6.投资组合优化1——sharpe最大  
104. #建立statistics函数来记录重要的投资组合统计数据（收益，方差和夏普比）  
105. #通过对约束最优问题的求解，得到最优解。其中约束是权重总和为1。  
106.   
107.   
108. def statistics(weights):  
109.   
110.     weights = np.array(weights)  
111.       
112.     port_returns = np.sum(returns.mean()*weights)*252  
113.       
114.     port_variance = np.sqrt(np.dot(weights.T, np.dot(returns.cov()*252,weights)))  
115.       
116.     return np.array([port_returns, port_variance, port_returns/port_variance])  
117.   
118. #最优化投资组合的推导是一个约束最优化问题  
119.   
120. import scipy.optimize as sco  
121.   
122. #最小化夏普指数的负值  
123.   
124. def min_sharpe(weights):  
125.   
126.     return -statistics(weights)[2]  
127.   
128. #约束是所有参数(权重)的总和为1。这可以用minimize函数的约定表达如下  
129.   
130. cons = ({'type':'eq', 'fun':lambda x: np.sum(x)-1})  
131.   
132. #我们还将参数值(权重)限制在0和1之间。这些值以多个元组组成的一个元组形式提供给最小化函数  
133.   
134. bnds = tuple((0,1) for x in range(noa))  
135.   
136. #优化函数调用中忽略的唯一输入是起始参数列表(对权重的初始猜测)。我们简单的使用平均分布。  
137.   
138. opts = sco.minimize(min_sharpe, noa*[1./noa,], method = 'SLSQP', bounds = bnds, constraints = cons)  
139.   
140. opts  
141.   
142. #得到的最优组合权重向量为：  
143. opts['x'].round(3)  
144.   
145. #sharpe最大的组合3个统计数据分别为：  
146. #预期收益率、预期波动率、最优夏普指数  
147. statistics(opts['x']).round(3)  
148.   
149.   
150. #7.投资组合优化2——方差最小  
151. #接下来，我们通过方差最小来选出最优投资组合。  
152. #但是我们定义一个函数对 方差进行最小化  
153.   
154. def min_variance(weights):  
155.   
156.     return statistics(weights)[1]  
157.   
158. optv = sco.minimize(min_variance, noa*[1./noa,],method = 'SLSQP', bounds = bnds, constraints = cons)  
159.   
160. optv  
161.   
162.   
163. #方差最小的最优组合权重向量及组合的统计数据分别为：  
164. optv['x'].round(3)  
165.   
166. #得到的预期收益率、波动率和夏普指数  
167. statistics(optv['x']).round(3)  
168.   
169.   
170.   
171.   
172. #8.组合的有效前沿  
173. #有效前沿有既定的目标收益率下方差最小的投资组合构成。  
174. #在最优化时采用两个约束，1.给定目标收益率，2.投资组合权重和为1。  
175.   
176. def min_variance(weights):  
177.   
178.     return statistics(weights)[1]  
179.   
180. #在不同目标收益率水平（target_returns）循环时，最小化的一个约束条件会变化。  
181.   
182. target_returns = np.linspace(0.0,0.5,50)  
183.   
184. target_variance = []  
185.   
186. for tar in target_returns:  
187.     cons = ({'type':'eq','fun':lambda x:statistics(x)[0]-tar},{'type':'eq','fun':lambda x:np.sum(x)-1})  
188.     res = sco.minimize(min_variance, noa*[1./noa,],method = 'SLSQP', bounds = bnds, constraints = cons)  
189.     target_variance.append(res['fun'])  
190.   
191. target_variance = np.array(target_variance)  
192. len(target_variance)  
193.   
194. #下面是最优化结果的展示。  
195. #叉号：构成的曲线是有效前沿（目标收益率下最优的投资组合）  
196. #红星：sharpe最大的投资组合  
197. #黄星：方差最小的投资组合  
198.   
199. plt.figure(figsize = (16,8))  
200.   
201. #圆圈：蒙特卡洛随机产生的组合分布  
202.   
203.   
204.   
205. plt.scatter(port_variance, port_returns, c = port_returns/port_variance,marker = 'o')  
206.   
207. #叉号：有效前沿  
208. len(target_variance),len(target_returns)  
209. plt.scatter(target_variance,target_returns, c = target_returns/target_variance, marker = 'x')  
210.   
211. #红星：标记最高sharpe组合  
212.   
213. plt.plot(statistics(opts['x'])[1], statistics(opts['x'])[0], 'r*', markersize = 15.0)  
214.   
215. #黄星：标记最小方差组合  
216.   
217. plt.plot(statistics(optv['x'])[1], statistics(optv['x'])[0], 'y*', markersize = 15.0)  
218.   
219. plt.grid(True)  
220.   
221. plt.xlabel('expected volatility')  
222.   
223. plt.ylabel('expected return')  
224.   
225. plt.colorbar(label = 'Sharpe ratio')  

 

·END· 

本文固定链接：http://www.liyonghua.com/?post=626
本文由liyonghua原创或编辑，互联分享,尊重版权,转载请以链接形式标明本文地址